ビッグデータやらアクセス解析やら。昨今は統計学が重要になりつつあるようだ。
一発奮起して学ぼうとしても、入門書の冒頭12ページあたりでつまづくこととなる。そう「分散」「標準偏差」で挫折してしまうのだ。この最初のハードルを自分なりの言葉で解説してみたいと思う。
さて。標準偏差とは…「バラつきの平均」のようなもの、である。うん。大雑把過ぎる。事例で説明してみよう。

［事例］：目黒店と渋谷店のどちらの店長になりたいか？
あなたはあるコンビニエンスストアを展開する企業の社員である。ある日、直営店の店長勤務を命じられた。店長職の空きは2つあり、ひとつは目黒店、もうひとつは渋谷店である。両店とも売上規模は同じ。どちらを選んでも良いとのことだ。さてどちらの店にしようか？

［前提］
・なるべく楽な店で働きたい

では、どのような店が楽なのだろうか？売上規模が同じなら、日々の売上にバラつきが無い方が仕入も予測しやすく楽そうに思える。

・売上にバラつきが無い方の店を選ぼう

［表で調べる］
半月分のデータを入手したので見比べてみる。

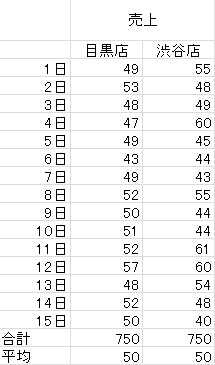
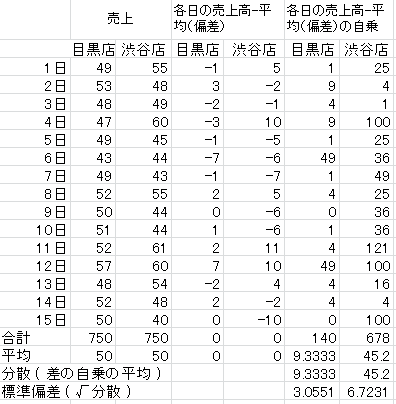
確かに売上の合計は同じ750万円、1日の平均売上は50万円とどちらも同じである。ただ数値だけでは「バラつき」具合はわかりづらい。

［グラフで調べる］
そこで数値をグラフ化してみる。

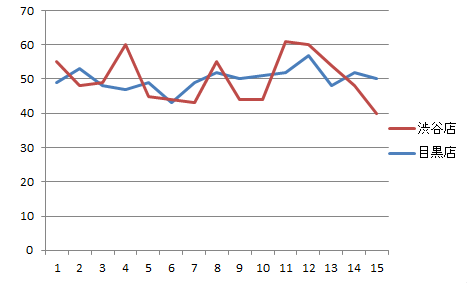
これを見ると、どちらの店も平均の50万円付近を中心に上下にデコボコしている。
ただそのバラつき具合は目黒店の方が幾分少ないように見える。

［数値化を試みる］
実際にどの程度バラつきの差があるのだろうか？

グラフでははっきりとした差がわかりにくい。数値で表現できないか？
そのために用いるのが「偏差」であり「分散」であり「標準偏差」である。

［偏差：各日の売上は平均からどれくらいかけ離れているか］
偏差とは平均との差である。その日の売上が平均からどのくらかけ離れているか、を表す。

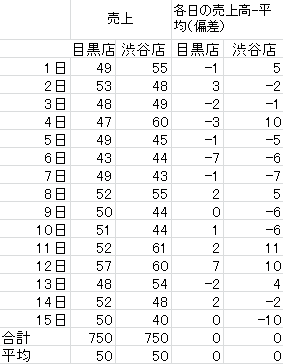
1日の目黒店の売上は49万円で平均50万円、-1万円が偏差となる。

渋谷店の4日の10万円や15日の-10万円はずいぶんと平均からかけ離れている。
やはり渋谷店の売上のバラつきが大きいことがわかる。

各日のバラつきはわかった。でも半月全体のバラつきはどのくらいなのだろうか？

［分散：半月全体では平均からどれくらいかけ離れているか（準備段階）］

半月全体のバラつき、とは偏差の平均である。

それを算出したいのであれば、偏差を合計してデータ数で割れば良い…のだが、各偏差はプラスとマイナスが混在している。そのため合計すると相殺されてしまうのだ（実際合計すると0になってしまう）。

そこで全てを正の数にするため、

１．偏差を自乗する

そして

２．「偏差の自乗」を合計する
３．「偏差の自乗」の合計をデータ数で割って平均を算出する

これが分散である。

目黒店では9.3万円、渋谷店では45.2万円となっている

全体で、どのくらいのバラつきがあるかの目安となるが、「偏差の自乗」を元に算出しているため、数値がかなり大きい（そこで標準偏差を用いることになる）。

［半月全体では平均からどれくらいかけ離れているか（完成段階）］
上記「分散」は『「自乗したものの合計」の平均』なので値が大きくなりすぎている。そこで、平方根にして「差の平均」を算出する。

目黒店：√9.3万円＝3.06万円
渋谷店：√45.2万円＝6.72万円

目黒店は渋谷店の約半分のバラつきである。

結果あなたはめでたく目黒店の店長就任となった
一日の売上は大体47万円～53万円程度の幅に収まりそうである。
これなら在庫管理も幾分予測しやすそうだ。快適な日々を過ごしていただきたい。

さて。長々と述べてきたが、なにぶん高校時代は数学劣等生だった私だ。思い違いもあるし数学的に正しくない言い回しもあると思うがご容赦いただきたい。私と同レベルの方の理解の手助けになれば幸いである。